
In the above problem, vertices of the image areħ. When we apply the formula, we will get the following vertices of the image (translated figure).Ħ. When we translate the given figure for (h, k) = (2, 3), we have to apply the formulaĥ. When we plot these points on a graph paper, we will get the figure of the pre-image (original figure).Ĥ. In the above problem, the vertices of the pre-image areģ. First we have to plot the vertices of the pre-image.Ģ.
#TRANSLATIONS GEOMETRY X Y HOW TO#
So, the rule that we have to apply here isīased on the rule given in step 1, we have to find the vertices of the translated triangle A'B'C'.Ī'(0, 4), B(4, 7) and C'(6, 5) How to sketch the translated figure?ġ. If this triangle is translated for (h, k ) = (2, 3) what will be the new vertices A', B' and C' ?įirst we have to know the correct rule that we have to apply in this problem. More often, however, geometry is moved into its final position using geometric transformations on the object itself or on its underlying CoordinateSystem. Example: to say the shape gets moved 30 Units in the 'X' direction, and 40 Units in the 'Y' direction, we can write: (x,y) (x+30,y+40) Which says 'all the x and y coordinates become x+30 and y+40'. Translation, Rotation, and Other Transformations Certain geometry objects can be created by explicitly stating x, y, and z coordinates in three-dimensional space. Coordinate plane rules: (x, y) (x ± h, y ± k) where h and k are the. Geometric transformations are bijections preserving certain geometric properties, usually from the xy-plane to itself but can also be of higher dimension. Translations are isometric, and preserve orientation. Translations can be achieved by performing two composite reflections over parallel lines. Let A(-2, 1), B(2, 4) and C(4, 2) be the three vertices of a triangle. Sometimes we just want to write down the translation, without showing it on a graph. Over the line y x: (x, y) (y, x) Through the origin: (x, y) (x, y) TRANSLATIONS: Translations are a slide or shift. Let us consider the following example to have better understanding of translation.
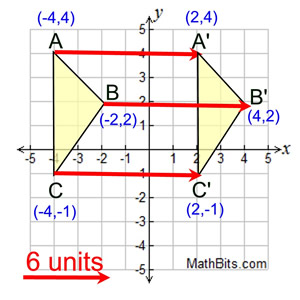

From the right-hand side of the matrix equation xPx' we have x 2x' + y' y x' + y' w 2x' + y' + w' Let us consider a circle x2 + y2 1. In a translation, you shift an image in coordinate space by adding a specified value to the x- and y-coordinates. That is, this projective transformation sends (1,0) on the xy-plane to the point at infinity in direction 1,-1>. When working with rotation matrix decompositions, specify the handedness of the rotation. A geometry translation is an isometric transformation, meaning that the original figure and the image are congruent. Obviously, this transformation sends (x,y,w)(1,0,1) to (x',y',w') (1,-1,0).The transformation f(x) (x+2) 2 shifts the parabola 2. This pre-image in the first function shows the function f(x) x 2. We can apply the transformation rules to graphs of quadratic functions. (x,y) (x-8, y-3) Transformation of Quadratic Functions.

Specify if the meaning is a rotation/translation of points or a rotation/translation of axes. This translation can algebraically be translated as 8 units left and 3 units down.Let \(\mathbf\right]\) Key Considerations


 0 kommentar(er)
0 kommentar(er)
